
|
AISpace2 | Main Tools | News | Downloads | Prototype Tools | Customizable Applets | Practice Exercises | Help | About AIspace |
|
|
Tutorials
Belief and Decision Networks
Tutorial Five (Supplementary): Conditional IndependenceThis tutorial gives a short introduction to the concepts of conditional independence and d-separation. For more in-depth information about these subjects, try some of the links listed at the end of this tutorial. A Bayesian network is a graphical representation of conditional independence and conditional probabilities. Informally, a variable is conditionally independent of another, if your belief in the value of the latter wouldn't influence your belief in the value of the former. By the same token, a variable is conditionally independent of another, given some information, if your belief in the value of the second variable wouldn't influence your belief in the value of the first, given that you have the information. For example, my belief in whether or not my cat has knocked over a plant on the balcony is independent of my belief in whether or not it is windy today. However, my belief in whether or not a plant on the balcony has been knocked over is not conditionally independent of either of these two factors, since either could be a cause of a plant being knocked over. Additionally, if I happen to know that a plant on my balcony has been knocked over, my belief in whether or not my cat has done it is no longer independent of my belief in whether or not it is windy. If it is windy, that gives me a reason to believe that the plant's being knocked over is a result of the wind. In other words, knowing that it is windy can explain away a reason for my plant's being knocked over. More formally, random variable X is independent of random variable Y given random variable Z, if P( X | Y & Z ) = P( X | Z ). One of the most important independence assumptions in a belief network is that each random variable is independent of its nondescendents given its parents. A broader formalisation is given by d-separation. The definition below is from [Pearl, 2000]: A path p is said to be d-separated (or blocked) by a set of nodes Z if and only if The algorithm used to determine irrelevant variables in Verbose Query Mode is the same algorithm used by the Quiz to determine the answers to conditional independence questions. To start quizzing yourself, click the 'Independence Quiz' button on the toolbar in Solve mode. The Quiz window will appear with a copy of the graph currently visible in the main applet. 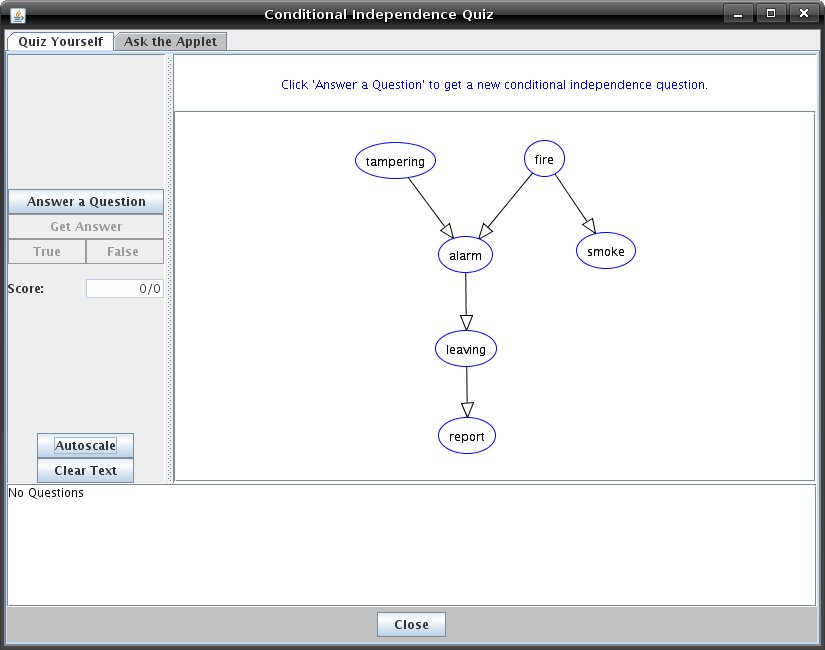 When the quiz window opens, the 'Quiz Yourself' tab will be selected. You will see a button labelled 'Answer a Question'. Below them will be some disabled options. There is also a text area at the bottom of the screen, where the questions you ask and answer will appear. If you click 'Answer a Question,' the applet will build a new question for you to answer and the question will appear in the text area below the graph canvas. The first node mentioned in the question will be outlined in red in the graph. The second will be outlined in pink. Any nodes that may appear in the question after this will be highlighted in blue. These blue highlighted nodes block the dependence between the two nodes originally selected. This is equivalent to claiming that these new nodes have observed values. This is to help you visualize the question being asked. You can will now be able to answer 'True' or 'False' by clicking on the corresponding buttons. Your score will be kept in the Score text area. If you are unsure of the answer to a question, you can click 'Get Answer' to get the answer. However, this of course will be counted as a wrong answer in your score. 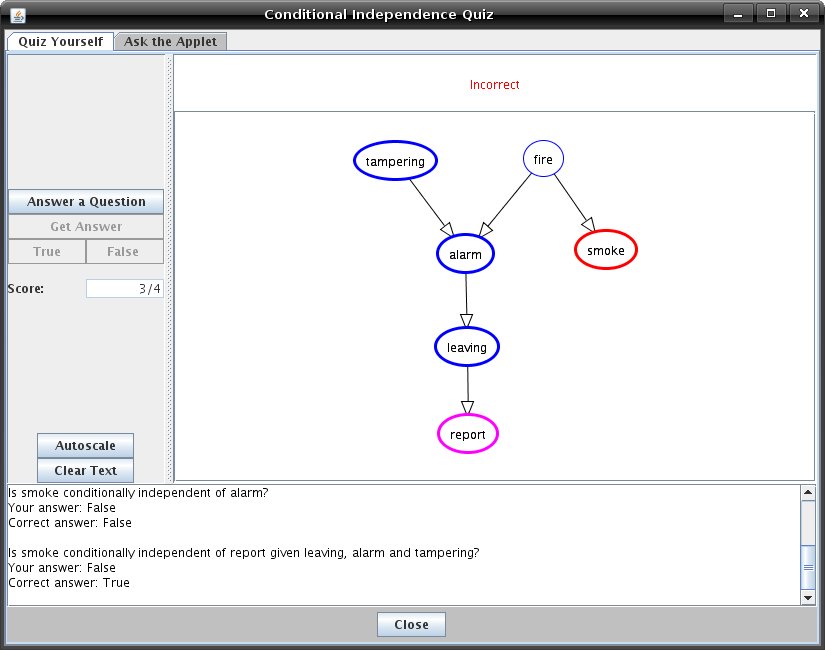 You can also ask the applet questions by clicking on the 'Ask the Applet' tab. Here, if you click the button labeled 'Ask a Question', the words above the graph canvas will read 'Select a node.' Click on a node, and it will become outlined in red. You should now see the instructions reading 'Select another node'. Notice that the question you are building appears in the text area as you select different nodes. When you select another node, it will be outlined in pink, and the instructions should read 'Now start selecting other nodes or click 'Get Answer'. Selecting other nodes will highlight those nodes in blue and follows the same scheme as described above for the 'Quiz Yourself' tab. Whenever you click 'Get Answer', which it should now be possible to do, the question you've been building will be answered. Click 'Get Answer' whenever you're ready, and you will see the answer to the question appear just after it in the text area at the bottom of the window. 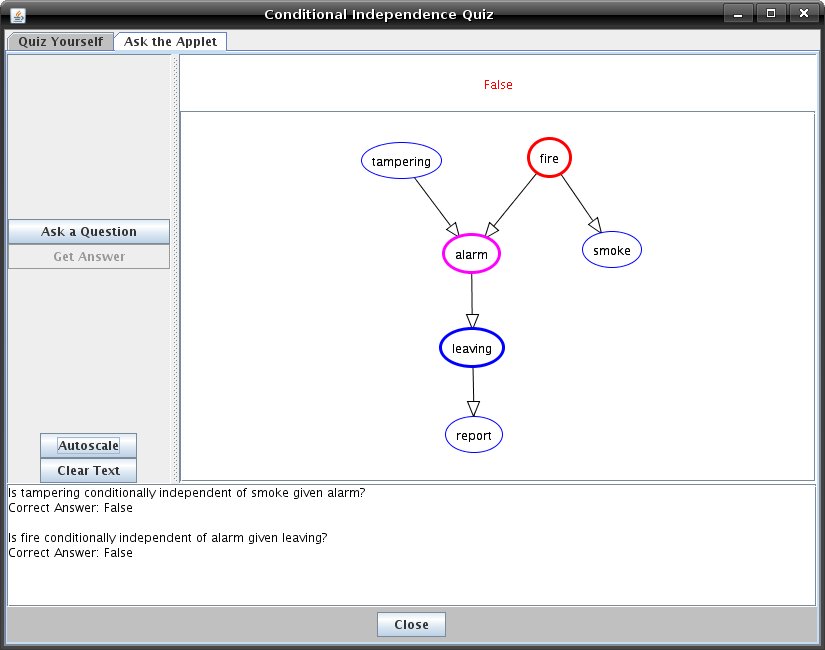 |
| Main Tools: Graph Searching | Consistency for CSP | SLS for CSP | Deduction | Belief and Decision Networks | Decision Trees | Neural Networks | STRIPS to CSP |