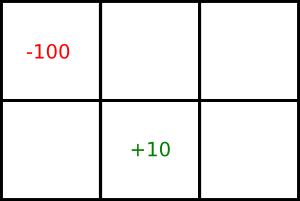|
Back to practice exercises.
1: Background Reading
2: Learning Goals
- Use the value iteration algorithm to generate a policy for a MDP problem.
- Modify the discount factor parameter to understand its effect on the value iteration algorithm.
- Use the asynchronous value iteration algorithm to generate a policy for a MDP problem.
3: Directed Questions
- What is the difference between infinite horizon and indefinite horizon problems? [solution]
- What is the difference between fully observable MDPs and POMDPs? [solution]
- What effect does decreasing the discount factor have on discounted reward? [solution]
- Does a indefinite horizon stationary MDP have a stationary optimal policy? [solution]
- In a stationary MDP, if an agent has a 20% chance of dying at each timestep, what is the optimal value for the discount factor? [solution]
4: Exercise: Gridworld
Consider the following grid world game:
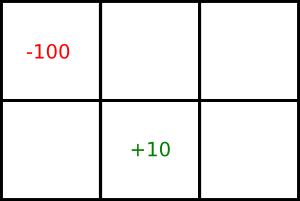
This is a stationary MDP with an infinite horizon. The agent can only be in one of the six locations. It gets the reward/punishment in a particular cell when it leaves the cell. It gets a reward of 10 for leaving the bottom-middle square and a punishment of 100 for leaving the top-left square. In each iteration of the game, the agent has to choose a direction to move. The agent can choose to move either up, down, left, or right. There is a 0.8 probability that it will move in that direction and a 0.1 probability that it will move in either of the neighboring directions. For example, if the agent wants to move up, there is a 0.8 probability that it will move up, a 0.1 probability that it will move left, and a 0.1 probability that it will move right. If the agent bumps into a wall, it stays in its current location and does not get any reward or punishment.
- Perform one step of value iteration and show the resulting value function for each state. Use an initial value of zero in each state and a discount factor of 0.9. [solution]
- What is the value in the top-left state after performing another step of value iteration? [solution]
- What is the optimal policy? [solution]
- What would the optimal policy be if the punishment in the top-left square was changed to each of the following values: 5, 0.0001, 0? [solution]
- Suppose we have the following values for the states:

If we select the top-left state and the action 'right', what is the value of Q[top-left,right] using asynchronous value iteration? Use a discount factor of 0.9 and the reward/punishment described in the original problem. [solution]
5: Learning Goals Revisited
- Use the value iteration algorithm to generate a policy for a MDP problem.
- Modify the discount factor parameter to understand its effect on the value iteration algorithm.
- Use the asynchronous value iteration algorithm to generate a policy for a MDP problem.
|